APIO 2021

Created2021-05-27Updated2021-05-27

第一次的國際賽，雖然不算到非常正式還是留個紀錄好了

賽前

因為可撥疫情，台北遊、捷絲旅和拉麵全部泡湯
原本以為可以睡晚一點是最值得高興的事，但還是6.半就不小心醒了= =
早上也沒做什麼，去買了巧克力和調那超難調的鏡頭位置就開始了

題目

不想看或看過的可以直接跳過owo

pA

題目

在一個由正六邊形拼成的平面上，一開始有一個人站在其中一個六邊形上，給定nn個行動，每筆行動會有一個方向和移動的距離LL，代表人會沿著該方向移動LL步
方向如下圖

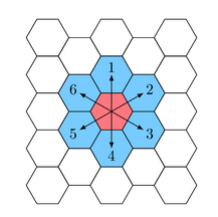
保證該路徑會有三個性質：

  1. 封閉的，代表起點位置和終點位置一樣
  2. 簡單的，除了起點外沒有重複的點
  3. 無遮蔽的，代表每一個路徑上的點都和至少一個非內部且不在此路徑上的點相鄰，內部的定義為在不經過路徑上的點的情況下，該點能走到的點的數量為有限

定義好點為路徑上的點或是內部的點
現在給定a,ba, b，定義一個好點xx的價值為a+d∗ba + d * b，其中dd為從起點開始只經由好點到達點xx的最近距離
請求出所有好點的價值和，模109+710^9 + 7

subtasks

對於任一筆，2≤n≤200000,∑i=1nL[i]≤109,1≤a,b≤1092 \leq n \leq 200000, \sum_{i = 1}^{n}L[i] \leq 10^9, 1 \leq a, b \leq 10^9

  1. n=3,b=0n = 3, b = 0，Score 3
  2. n=3n = 3，Score 6
  3. ∑i=1nL[i]≤2000\sum_{i = 1}^{n}L[i] \leq 2000，Score 11
  4. b=0,∑i=1nL[i]≤200000b = 0, \sum_{i = 1}^{n}L[i] \leq 200000，Score 12
  5. b=0b = 0，Score 15
  6. ∑i=1nL[i]≤200000\sum_{i = 1}^{n}L[i] \leq 200000，Score 19
  7. ∀0≤i≤n−2,L[i]=L[i+1]\forall 0 \leq i \leq n - 2, L[i] = L[i + 1]，Score 18
  8. 無其他限制，Score 16
pB

題目

有一個長度為nn的permutation hh，當你位於位置ii的時候可以移動到兩個位置：

  1. 所有滿足j<i,h[j]>h[i]j < i, h[j] > h[i]的數中的最大值
  2. 所有滿足j>i,h[j]>h[i]j > i, h[j] > h[i]的數中的最小值

定義dis(i,j)dis(i, j)為從ii走到jj的最短距離，現在給定qq筆詢問，每筆詢問給定a,b,c,da, b, c, d，滿足a≤b<c≤da \leq b < c \leq d，請回答min⁡a≤s≤b,c≤e≤ddis(s,e)\min_{a \leq s \leq b, c \leq e \leq d}{dis(s, e)}，若無法走到則輸出−1-1

subtasks

對於任一筆，2≤n≤200000,1≤q≤1000002 \leq n \leq 200000, 1 \leq q \leq 100000

  1. ∀0≤i≤n−1,h[i]=i+1\forall 0 \leq i \leq n - 1, h[i] = i + 1，Score 4
  2. n≤200,q≤200n \leq 200, q \leq 200，Score 8
  3. n≤2000,q≤2000n \leq 2000, q \leq 2000，Score 13
  4. q≤5q \leq 5，Score 12
  5. a=b,c=da = b, c = d，Score 23
  6. c=dc = d，Score 21
  7. 無其他限制，Score 19
pC

題目

給定一棵nn個點的有權樹，請對於所有0≤k≤n−10 \leq k \leq n - 1，輸出最少需要移除的邊的權重和才能使這棵樹的每個點的度數≤k\leq k

subtasks

對於任一筆，1≤n≤10000001 \leq n \leq 1000000

  1. 星狀圖，Score 5
  2. 樹是一條鍊，Score 7
  3. n≤200n \leq 200，Score 14
  4. n≤2000n \leq 2000，Score 10
  5. 邊的權重=1= 1，Score 17
  6. 邊的權重≤10\leq 10，Score 25
  7. 無其他限制，Score 22

比賽情況

開場一樣先看完題目

pA 噁題
pB 單調對列 然後就沒有了
pC 一臉樹dp / greedy

然後發現subtasks都切好細www，感覺蠻好玩的，有種真的可以把每一筆當一題的感覺

覺得pB最可做就先想pB了，先測了一下grader，丟了第一筆之後就很快想到一個O(nq)\mathcal{O}(nq)的解，寫完後de了一下bug拿到前四筆

之後寫了pC，一樣測grader拿了前兩筆，對O(n2)\mathcal{O}(n^2)還沒啥想法就先丟著

之後寫了pA，因為認定是噁題就直接喇分，然後搞錯題目意思好久，才拿到前兩筆

pA: 9/ pB: 37/ pC: 12

之後回去輪流想了pB / pC，pC想到了一個O(n2)\mathcal{O}(n^2)的dp，寫完之後因為judge很慢(這時還沒rejudge喔)，就亂claim了一個第五筆的greedy，寫完後直接丟

過不久發現兩個都0分= =
就開始de了一下dp，發現一種轉移寫爛，改完之後過第三和第四筆

pA: 9/ pB: 37/ pC: 36

之後回去想pB第五筆，發現他的問題是全點對最短路，根本不可能做
之後想起忘記誰說過發現題目不可做就要觀察性質，於是觀察了一陣子發現特別的性質，用了兩個倍增寫掉

pA: 9/ pB: 60/ pC: 36

原本應該要換題了，但我感覺第五筆要推到第六筆不難就繼續想了(?
想了一下claim了起點只會有三個就開寫了，寫完傳
然後傳完之後就發了announcement說judge很慢，請耐心等待(?
嘛 反正我也只多傳一筆，就沒管那麼多

之後pB滿分感覺很難就先丟著，輪流想pA / pC
pA我盯著之前寫下的座標轉換，想了一下發現
不對R，第四筆和第五筆不就只是問格子點數量而已
剛好之前1!有聽說一個東西叫皮克定理，也有寫過問多邊形格子點的題目，而又剛好APIO可以貼以前寫過的code，諸多巧合之下就很愉悅的直接貼了code傳上去
嘛 還在in queue，而且不知道為什麼judge還火力全開開始rejudge了(?
感覺要等很久，看了一下時間大概剩半小時決定繼續喇pA第三筆
然而有點線段相交中毒一直卡在O(n3)\mathcal{O}(n^3)的作法
之後等了一下發現延長半小時
同時我也想到壓到O(n2)\mathcal{O}(n^2)的作法，寫了好一陣子之後丟，發現pB的第六筆跑完了，沒過，好慘= =
pA的格子點過了則是預料中的事

pA: 36/ pB: 60/ pC: 36

剩下的時間就輪流想pB第六筆和pC第五筆，貌似因為judge還沒跑完所以又延了半小時
好嗨，這可能是唯一一次能夠打到六個小時比賽的機會了吧= =
後來pA的第三筆也過了

pA: 47/ pB: 60/ pC: 36

之後pC貌似想到了一個分case暴力的解法，但我不會greedy的部分，很難過的繼續燒雞
pB最後五分鐘推出了感覺正確的結論，但根本來不及寫就結束了= =

最後就收在47/60/36
感覺算普普通通，不過我覺得我該拿的分都有拿到，所以也蠻滿意的

最後填成績的時候有點嚇到，好像很多人都因為judge燒雞了，莫名其妙拿了一個TWN rk2，不過還有一個原因是pA只有我有拿到格子點的subtask= =
不過也只有我pB有寫第五筆但沒拿到第六筆，爛死= =
(賽後發現其實第五筆要推到第六筆其實很簡單，但我賽中就是耍智障沒想到= =)

結果

Score: 143
TWN rk2, total rk49，銀牌
牌線：84 / 136 / 209

算運氣不錯吧，比銀牌線高了一點，撈到了銀牌

不過還是有點空虛的感覺@@
拿了銀牌好像也沒有甚麼用= =

高二競程只剩下不知道會不會取消的YTP了，希望能打好> <